odd function integration | Iba pa

Now, I am not here to give you an illusion of control. When I say that a lottery game is mathematically predictable to an extent, it doesn’t mean we can predict the next winning numbers. You cannot predict the next winning numbers. No one can. 13. But with probability theory, you can make an informed choice based on how the lottery .

odd function integration*******An odd function is one in which f (−x)= −f (x) f ( − x) = − f ( x) for all x x in the domain, and the graph of the function is symmetric about the origin. Integrals of even functions, when the limits of integration are from − a a to a a, involve two equal areas, because they are . Sometimes we can simplify a definite integral if we recognize that the function we’re integrating is an even function or an odd function. If the function is neither . For an odd function, I know that f(x) = - f(x). I'm trying to show that $\int^{a}_{-a} f(x) dx$ = 0. I've seen the proof where it splits the integral up into: .

Now, let’s dig into integrals of even and odd functions! Let f be an integrable function on some closed interval that is symmetric about zero — for example [ − a, a], for a ≥ 0. If f is .

Let $f$ be an odd function with a primitive on the open interval $\openint {-a} a$, where $a > 0$. Then the improper integral of $f$ on $\openint {-a} a$ is: $\ds .

An odd function is one in which \(f(−x)=−f(x)\) for all \(x\) in the domain, and the graph of the function is symmetric about the origin. Integrals of even functions, when the limits of . Example 1.2.11 Odd functions. Three examples of odd functions are \(f(x)=\sin x\text{,}\) \(f(x)=\tan x\) and \(f(x)=x^3\text{.}\) In fact, if \(f(x)\) is any odd power .Symmetry appears throughout mathematics in many different forms, and its use often leads to insights and efficiencies. Here we use the symmetry of a function to simplify integral calculations. Section 1.1 introduced .

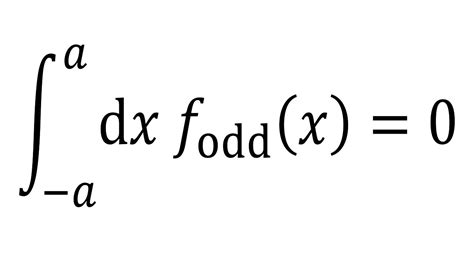
Integrating even and odd functions involves finding the definite integral of a function over a symmetric interval. For even functions, the integral over a symmetric interval is .Iba paIntegrating even and odd functions involves finding the definite integral of a function over a symmetric interval. For even functions, the integral over a symmetric interval is .Integrating Odd Functions on Symmetric Intervals. Since on one side of the origin the function is negative but has the same y-values as on the other side of the origin, areas under the curve cancel out over .2. Start by splitting the integral into two pieces, the part over negatives values of x and the part over positive values. ∫2 − 2f(x)dx = ∫0 − 2f(x)dx + ∫2 0f(x)dx. From here you can apply the definition of an even or odd function. Cite. answered Feb 13, .

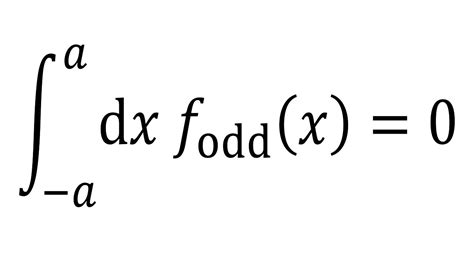
They are special types of functions. Even Functions. A function is "even" when: f(x) = f(−x) for all x In other words there is symmetry about the y-axis (like a reflection):. This is the curve f(x) = x 2 +1. They are . Theorem 1.2.1 Arithmetic of Integration. Let a, b and A, B, C be real numbers. Let the functions f(x) and g(x) be integrable on an interval that contains a and b. Then. (a) ∫b a(f(x) + g(x))dx = ∫b af(x)dx + ∫b ag(x)dx (b) ∫b a(f(x) − g(x))dx = ∫b af(x)dx − ∫b ag(x)dx (c) ∫b aCf(x)dx = C ⋅ ∫b af(x)dx. Combining these three . 1. This is true provided the integral is interpreted as Cauchy principal value. Since f f is odd, ∫A −A f(x)dx = 0 ∫ − A A f ( x) d x = 0. Hence, p. v.∫∞ −∞ f(x)dx = limA→∞∫A −A f(x)dx = 0 p. v. ∫ − ∞ ∞ f ( x) d x = lim A → ∞ ∫ − A A f ( x) d x = 0. There's also the implicit assumption that f f is .odd function integration Iba pa The integration of an odd function over a symmetric interval can be understood through some fundamental concepts in calculus and symmetry. An odd function is defined as a function f (x) f ( x) that satisfies the condition f (−x) = −f (x) f ( − x) = − f ( x) for all x x in the domain of the function. Graphically, odd functions exhibit .The theorem of “Integration of Even and Odd Functions” is a way to find integrals for odd and even functions. It’s a method that makes some challenging definite integrals easier to find. In order to use it, you have to be evaluating a function over an interval that’s either symmetric about the origin or symmetric about the y-axis [1]. Prove that a symmetric integral of an odd function is zero. This is true if the limits go from -a to a.I've got tons of integrals in my integrals playlist! C.

Get your Crossfire loads here in Shop4fun!

odd function integration|Iba pa